前言;虽然小孩现在只有1岁半,计划今后与孩子在学习上共同进退,同时如果有一样的家长或在准备的高考的同学,希望留言或提供方法及心得;通过真题的解释与知识的收集一来是与大家共享,二来也是为了教小孩做好学习准备。如果你自己都克服或理解不了的困难,那么要求孩子去解决去发现其实也不公平。
1.高考数学选择题的解法第一个应该想到的是代入法。即把以上答案直接代入判断,这样会比较节省时间。上述如果代入的话。
题目要求集合M与集合N的交集为0;就要算出集合N中的X为多少才能满足0这个要求。
A:先把-2代入到N的公式中,-2可以满足,其它-1与0与1代入去都是小于0的,即可以排除A
B及D:与A共理完可以排除。
因此答案为C。
有些同学在做选择题时当大题来做的话就很花费时间,因为要告诉孩子,选择尽量使用代入法(图像法/逻辑法等)。不然会影响后面的做题效率。
我们在高考复习时,为了更有针对性地学习,一定要理解高考的数学大纲,这样才能有重点复习,这样我们可以在确保我们知道考试会考什么内容,那些内容大概率会出选择题,那些内容大概率会出分析题等高分题,由于考卷有限,基本上的知识点基本上都没涉及到。
下述内容为2023年广东高考数学大纲里的内容:
高考数学必考内容包括:集合(集合的含义与表示,集合间的基本关系,集合的基本运算)
第一题其实就是考集合的知识点,好了既然我们已通过代入法去解决问题了,那么就开始学习高考大纲的知识点吧。
集合的含义:元素的组成的总体叫作集合(简称为集)。
什么是元素:元素是集合的对象,根据集合的定义,元素可以是不是同的东西。
(例如下述例子中的集合A,同学与老师就是集合A的元素)
交集:即不同的集同里是否有相同的元素。
(例如下述例子;集合A与集同B的人完全不一样就是不相交,如果有部分一样就是部分相交)
如何让孩子更好理解集合呢?毕竟对于第一次接触这些名词时都比较抽象;好么我们可以向孩子举个例子说:
例1:集合A与集合B有一个交集
A班有50个同学+一个数学老师(庄小燕)为集合A
B班有50个同学+一个数学老师(庄小燕)为集合B
那么A班的50个同学与老师就叫为集合A的元素;同理B也一样
上述集合A与集合B都有同一个元素数学老师(庄小燕);
备注:有时小孩会占牛角钻说A班与B班也有同一个同学,这情况可以具体情况给他具体解释,不能完全否定孩子。
例子2:集合A与集合B有没有交集
A班有50个同学+一个数学老师(庄小燕)为集合A
B班有50个同学+一个数学老师(李小明)为集合B
因为A班同学与老师完全不一样,所以上述是没有交集的。
一开始学集合时,不适宜一下子说得太复杂或太抽象。因此通过上面的例子让孩子理解集合的基本含义就很重要了。

理解了集合的基本概念后就要知道,在书本上一般是如果表示集合的。
集合的表示方法一般如下:
1.列举法
2.描述法
3.图像法(通过图像进行对比)
4.符号法(通过符号来描述)
例如下述2023广东高考数学真题的中集M为就是列举法。
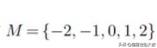
通大括号把四个元素一一列出来即M就是集合,也可以叫集合M;它的元素为-2,-1,0,2
而集合N呢则为描述法,它通不等式公式来描述即它的集合元素只要满足下面的公式都是它的元素。
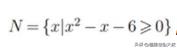
为了方便要下;再把题目复制在下面供参考:

上述题目分别交待了,集合M与集合N后,题目要就要求它的交集。
这里考的就是集合的运算,因此就要懂什么是交集的运算符号了。
下面是的知识点就是集合的运算常用表示方法:
(1)交集:如真题中,集合M与集N的交集如果用运算符号表示就是:M∩N。即交集的运算符号为∩。
(2)并集:集合A与集合B,把它们全部的要素合为一起组合而成的集合,称之为集合A与集合B的交集并集,记作A∪B。这个有点抽象,可以举例子,集合A是A集,集合B为B集,那么集合A与集合B的并集就是A班+B班的总和。
下述集合的其它运算常用方式,一开始不能说得太复杂,应该一步一步提升。
(3)相对补集:若A和B是集合,则A在B中的相对补集在这种一个集合:其要素归属于B但不属于A,B-A={x|x∈B且xA}。
(4)一定补集:若给出合集U,有AU,则A在U中的相对补集称之为A的一定补集(或通称补集),可以写成UA。
(5)子集合:子集合是一个数学概念:倘若集合A的任何一个要素全是集合B的要素,因此集合A称之为集合B的子集合。集合符号:若a∈A,均有a∈B,则AB。
结尾处再总结一次:
高考大纲的集合为必考考点,一般出选择题的概率会高。
大纳如下:
集合(集合的含义与表示,集合间的基本关系,集合的基本运算)
2023真题如下:

先把上述基础学习了,以后再深入学习。
一般情况每科都合格以上,总分基本能达到本科线了,加油。
