线性回归和逻辑回归是两种常用的机器学习算法,它们都属于广义线性模型的特例,但也有很多区别。下面是一些主要的区别:线性回归用于回归问题,逻辑回归用于分类问题。回归问题是指预测一个连续的数值变量,如房价、
线性回归和逻辑回归是两种常用的机器学习算法,它们都属于广义线性模型的特例,但也有很多区别。下面是一些主要的区别:
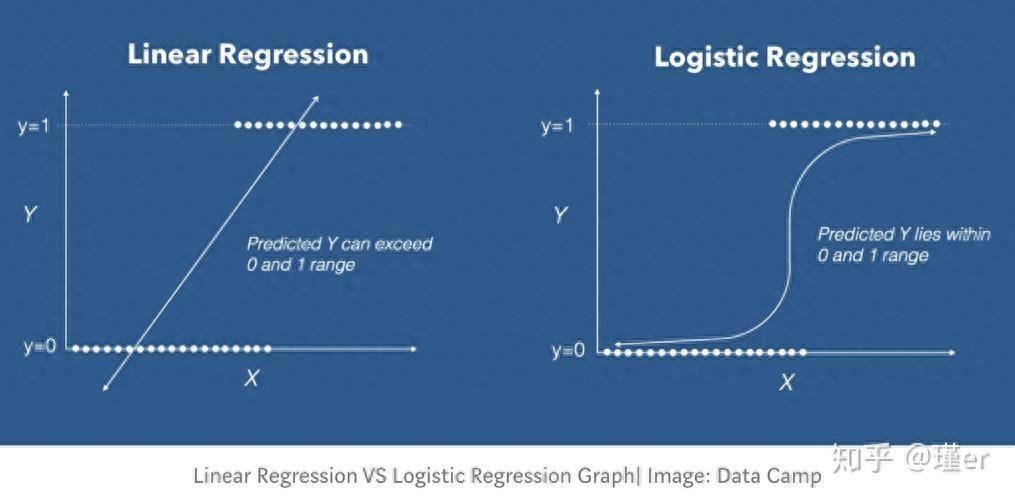
- 线性回归用于回归问题,逻辑回归用于分类问题。回归问题是指预测一个连续的数值变量,如房价、温度、身高等;分类问题是指预测一个离散的类别变量,如是或否、男或女、苹果或香蕉等。
- 线性回归的输出变量是连续的,逻辑回归的输出变量是离散的。线性回归的输出变量可以取任意实数值,逻辑回归的输出变量只能取有限个数的值,通常是0或1,表示两个类别。也可以有多个类别,但需要用到多项式逻辑回归或者一对多的策略。
- 线性回归要求自变量和因变量呈线性关系,逻辑回归不要求自变量和因变量呈线性关系。线性关系是指自变量和因变量之间可以用一条直线来描述,如y=ax+b;非线性关系是指自变量和因变量之间不能用一条直线来描述,如y=ax^2+bx+c。
- 线性回归要求变量服从正态分布,逻辑回归对变量分布没有要求。正态分布是指变量的概率密度函数呈钟形曲线,如高斯分布;非正态分布是指变量的概率密度函数不呈钟形曲线,如均匀分布、泊松分布等。
- 线性回归使用最小二乘法作为参数估计方法,逻辑回归使用极大似然法作为参数估计方法。最小二乘法是指使得预测值和实际值之间的平方误差之和最小;极大似然法是指使得观测数据出现的概率最大。
本站部分文章来自网络或用户投稿,如无特殊说明或标注,均为本站原创发布。涉及资源下载的,本站旨在共享仅供大家学习与参考,如您想商用请获取官网版权,如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。
