古希腊人使用两套书写系统表示数字,一种是所谓的「阿提卡系统」,又叫赫罗狄安系统」,因二世纪的语法学家赫罗狄安(Αἴλιος Ἡρωδιανός)曾对其撰文介绍。另一种是 「爱奥尼亚系统」,又因其可能最早出现于米利都而被称为「米利都系统」。不过他给的那个转换器提供的是现代希腊语的数字转写结果,虽然是建立于爱奥尼亚系统之上,但与古代用法还是存在差异。
1、Acrophonic numerals直译是“首字母数字”,因为起源于阿提卡地区,也被称为阿提卡数字
阿提卡系统成型于古风时代,但最早的证据来自前五世纪的雅典,属于比较典型的截头表音(acrophonic)系统,因此以字母Δ开头的10(δέκα)记作Δ,以字母Η开头的100(ἑκατόν)记作Η,以字母Χ开头的1,000(χίλιοι)记作Χ,以字母Μ开头的10,000(μύριοι)记作Μ,以此类推。这一规则存在两个例外,一个是数字1到9,另一个是作为中介数的 :
- 1使用一竖(Ι)表示,2-9分别记作II、III、IIII、Π、ΠI、ΠII、ΠIII、ΠIIII
数字5(πέντε)截头记作Π(其实更准确的应该是U+10143, ,字母Π的旧体), 记作 (U+10144;顾名思义, ), 记作 (U+10145;顾名思义, ), 记作 (U+10146;顾名思义, ), 记作 (U+10147;顾名思义, )

Unicode不兼容的请看本图
举例:数字114514可记作ΔIΜΧΧΧΧ ΔIIII(阿提卡系统内没有比Μ更大的基数;古代日常使用中也很少碰到这么大的数字)
需要注意的是这一系统从未被标准化,因此在各地都存在不同变体;Unicode中收录的符号基本是以阿提卡体为原型的。另外以上这五个符号在特定用途下亦存在变体,例如计钱款数量与货品称重时会加上字母Τ或Σ,分别代表货币单位塔兰同/τάλαντον与质量单位斯塔特/στατήρ。
50000
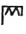
这种数字的书写规则和后来的罗马数字基本完全相同,比如4999写作:
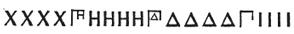
值得注意的是,阿提卡系统绝不是希腊地区“标准”的数字系统。当时希腊各地区用的字母多少都有点差别,由首字母产生的数字自然也不尽相同。
2、爱奥尼亚系统成型更晚,一般认为在前五至前三世纪间。与前者相比,首先是多了三个古典希腊字母表内已经不存在的字母:表示6的ϛ(注意和ς不是一个字母),表示90的ϟ,和表示900的ϡ,以弥补使用只有24个字母的希腊字母表代表27个数字(9个「一」,9个「十」与9个「百」)时的不足。书写大于999的数字,则在代表1-9的数字符号前加一点以表示「千」,因此6,000写作͵ϛ;书写大于9999的数字时,可以在代表1-9的数字符号上加二点以表示「万」,因此30,000可写作γ̈,或者可以使用表「万」的基数M,在M顶上添加序数,例如表示30,000可在M上添一个γ。注意到后一种计数法和阿波罗尼奥斯用来记大数的方式类似,例如360,000,000,000可以记作:
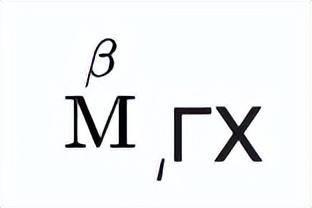
alphabetic numerals
直译是“字母数字“,就是把27个希腊字母按顺序排列,前九个代表1~9,中间九个代表10~90,最后九个代表100~900。

千位数字通过在原先的字母前面加个撇(撇可上可下)或者强送气符(“”)表示,也有些写法会把撇和字母合在一起。比如1000可以写作Ά
或者
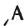
或者Ἁ
或者
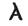
一万并不是写作Ί,而是借用阿提卡数字中的M表示。两万写作ΒΜ,MB或者把B写在M上面。
更大的数字似乎就没有通用的规范了,不同地域、时代的作者采用了很多种不同的写法
比如前三世纪的天文学家,Aristarchus of Samos,作品中的71755875写作:
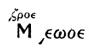
公元前后的数学家Heron用分音符(就是头上两个点)区分万位以上的数字,在他的Geometrica中18592写作:
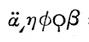
(17.33)
公元三世纪的Diophantus则会把万位以上的数字写在M右边,之后用一个圆点和万位以下的数字隔开。他的1507984写作:
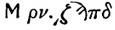
(IV.28)
阿基米德在《数沙者》(Ψαμμίτης)里提出过一个专门用来表示大数的八进位系统,第一阶为1到 ,第二阶到 ,以此类推,直到第 阶为止记为第一周期,之后为第二周期,直至第 ….周期。但这个系统未被阿基米德以外的任何人所采用。
古希腊人表示分数时的记法与现代没有多少差异,可以参考前面答主的。一些作者会选择口述分数而不使用符号,例如
可以文字写作τρία πέμπτα。另外天文学家有专门一套沿用自巴比伦人的六十进位系统:一度(μοῖραι)为60分(λεπτά),一分为60秒(δεύτερα ἑξηκοστά),等等;这一系统内还存有一个表示零的符号: ,一般认为是「无」(οὐδέν)的缩写。
